什么叫代数式(代数式的定义是什么)
初中数学知识点:
实数部分
一、实数与数轴
1、数轴:规定了原点、正方向、单位长度的直线称为数轴。原点、正方向、单位长度是数轴的三要素。
2、数轴上的点和实数的对应关系:数轴上的每一个点都表示一个实数,而每一个实数都可以用数轴上的唯一的点来表示。实数和数轴上的点是一一对应的关系。
二、实数大小的比较
1、在数轴上表示两个数,右边的数总比左边的数大。
2、正数大于0;负数小于0;正数大于一切负数;两个负数绝对值大的反而小。
三、实数的运算
1、加法:
(1)同号两数相加,取原来的符号,并把它们的绝对值相加;
(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。可使用加法交换律、结合律。
2、减法:减去一个数等于加上这个数的相反数。
3、乘法:
(1)两数相乘,同号取正,异号取负,并把绝对值相乘。
(2)n个实数相乘,有一个因数为0,积就为0;若n个非0的实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数为奇数个时,积为负。
展开全文
(3)乘法可使用乘法交换律、乘法结合律、乘法分配律。
4、除法:
(1)两数相除,同号得正,异号得负,并把绝对值相除。
(2)除以一个数等于乘以这个数的倒数。
(3)0除以任何数都等于0,0不能做被除数。
5、乘方与开方:乘方与开方互为逆运算。
6、实数的运算顺序:乘方、开方为三级运算,乘、除为二级运算,加、减是一级运算,如果没有括号,在同一级运算中要从左到右依次运算,不同级的运算,先算高级的运算再算低级的运算,有括号的先算括号里的运算。无论何种运算,都要注意先定符号后运算。
7、自然数:零和正整数统称为自然数。
8、素数:在大于1的自然数中,只能被1和其自身整除的数叫素数,又称质数。
9、相反数:绝对值相同而符号相反的两个数,互称为相反数,零的相反数是零
10、倒数:零没有倒数,1除以某个数(不为零)所得的商称为这个数的倒数。
11、运算率:设abc为实数,则有:
交换率:a+b=b+a
结合律:a+(b+c)=(a+b)+c
乘法对加法的分配率:a.(b+c)=ab+ac
运算顺序:在一个式子里,先乘方、开方,然后乘除,最后加减,有括号时,由最里层的括号算起,逐层去掉括号,有时根据运算率可改变上述顺序。
代数部分
代数式
基础知识点:
一、代数式
1、代数式:用运算符号把数或表示数的字母连结而成的式子,叫代数式。单独一个数或者一个字母也是代数式。
2、代数式的值:用数值代替代数里的字母,计算后得到的结果叫做代数式的值。
3、代数式的分类:代数式分有理式和无理式;有理式又分整式和分式;整式分单项式和多项式。
二、整式的有关概念及运算
1、概念
(1)单项式:数与字母的积叫做单项式。单独一个数或字母也是单项式。
单项式的次数:一个单项式中,所有字母的指数叫做这个单项式的次数。
单项式的系数:单项式中的数字因数叫单项式的系数。
单独的一个字母或数字也叫单项式。
(2)多项式:几个单项式的(代数)和叫做多项式。
多项式的项:多项式中每一个单项式都叫多项式的项。一个多项式含有几项,就叫几项式。
多项式的次数:多项式里,次数最高的项的次数,就是这个多项式的次数。不含字母的项叫常数项。
升(降)幂排列:把一个多项式按某一个字母的指数从小(大)到大(小)的顺序排列起来,叫做把多项式按这个字母升(降)幂排列。
(3)同类项:所含字母相同,并且相同字母的指数也分别相同的项叫做同类项。
2、运算
(1)整式的加减:
合并同类项:把同类项的系数相加,所得结果作为系数,字母及字母的指数不变。
去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变;括号前面是“–”号,把括号和它前面的“–”号去掉,括号里的各项都变号。
添括号法则:括号前面是“+”号,括到括号里的各项都不变;括号前面是“–”号,括到括号里的各项都变号。
整式的加减实际上就是合并同类项,在运算时,如果遇到括号,先去括号,再合并同类项。
(2)整式的乘除:
单项式乘以单项式:用它们系数的积作为积的系数,对于相同的字母,用它们的指数的和作为这个字母的指数;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式乘以多项式:就是用单项式去乘多项式的每一项,再把所得的积相加。
多项式乘以多项式:先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。(a+b)(c-d)=ac-ad+bc-bd
乘法公式:平方差公式:(a+b)(a-b)=a^2-b^2(a^2表示a的平方);
完全平方公式:(a±b)^2=a^2±2ab+b^2,
三、因式分解
1、因式分解概念:把一个多项式化成几个整式的积的形式,叫因式分解。
2、因式分解的一般步骤:
(1)如果多项式的各项有公因式,那么先提公因式;
(2)提出公因式或无公因式可提,再考虑可否运用公式或十字相乘法;
(3)对二次三项式,应先尝试用十字相乘法分解,不行的再用求根公式法。
(4)最后考虑用分组分解法。
四、分式
1、分式定义:形如A/B(B≠0)的式子叫分式,其中A、B是整式,且B中含有字母。
(1)分式无意义:B=0时,分式无意义;B≠0时,分式有意义。
(2)分式的值为0:A=0,B≠0时,分式的值等于0。
(3)分式的约分:把一个分式的分子与分母的公因式约去叫做分式的约分。方法是把分子、分母因式分解,再约去公因式。
(4)最简分式:一个分式的分子与分母没有公因式时,叫做最简分式。分式运算的最终结果若是分式,一定要化为最简分式。
(5)通分:把几个异分母的分式分别化成与原来分式相等的同分母分式的过程,叫做分式的通分。
(6)最简公分母:各分式的分母所有因式的最高次幂的积。
(7)有理式:整式和分式统称有理式。
2、分式的基本性质:
(1)分式的分子、分母同时乘以或除以一个非零整式,所得值不变。
(2)分式的变号法则:分式的分子,分母与分式本身的符号,改变其中任何两个,分式的值不变。
3、分式的运算:
(1)加、减:同分母的分式相加减,分母不变,分子相加减;异分母的分式相加减,先把它们通分成同分母的分式再相加减。
(2)乘:先对各分式的分子、分母因式分解,约分后再分子乘以分子,分母乘以分母。
(3)除:除以一个分式等于乘上它的倒数式。
(4)乘方:分式的乘方就是把分子、分母分别乘方。
五、二次根式
1、二次根式的概念:略。
最简二次根式:被开方数的每一个因式的指数都小于根指数2,并且被开方数不含分母的二次根式叫做最简二次根式。
二次根式运算的最终结果如果是根式,要化成最简二次根式。
代数部分
方程和方程组
基础知识点:
一、方程的有关概念
1、方程:含有未知数的等式叫做方程。
2、方程的解:使方程左、右两边的值相等的未知数的值叫方程的解,含有一个未知数的方程的解也叫做方程的根。
3、解方程:求方程的解或方判断方程无解的过程叫做解方程。
4、方程的增根:在方程变形时,产生的不适合原方程的根叫做原方程的增根。
二、一元方程
1、一元一次方程
(1)一元一次方程的标准形式:ax+b=0(其中x是未知数,a、b是已知数,a≠0)
(2)一元一次方程的最简形式:ax=b(其中x是未知数,a、b是已知数,a≠0)
(3)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项和系数化为1。
(4)一元一次方程有唯一的一个解。
2、一元二次方程
(1)一元二次方程的一般形式:ax^2+bx+c=0(其中x是未知数,a、b、c是已知数,a≠0)
(2)一元二次方程的解法:直接开平方法、配方法、公式法、因式分解法
(3)一元二次方程解法的选择顺序是:先特殊后一般,如没有要求,一般不用配方法。
(4)一元二次方程的根的判别式:
当Δ>0时,方程有两个不相等的实数根;
当Δ=0时,方程有两个相等的实数根;
当Δ< 0时,方程没有实数根,无解;
当Δ≥0时,方程有两个实数根
(5)一元二次方程根与系数的关系:
若x1,x2,是一元二次方程ax^2+bx+c=0(a≠0)的两个根,那么:
x1+x2=-b/a, x1.x2=c/a.
三、分式方程
(1)定义:分母中含有未知数的方程叫做分式方程。
(2)分式方程的解法:
一般解法:去分母法,方程两边都乘以最简公分母。
特殊方法:换元法。
(3)检验方法:一般把求得的未知数的值代入最简公分母,使最简公分母不为0的就是原方程的根;使得最简公分母为0的就是原方程的增根,增根必须舍去,也可以把求得的未知数的值代入原方程检验。
四、方程组
1、方程组的解:方程组中各方程的公共解叫做方程组的解。
2、解方程组:求方程组的解或判断方程组无解的过程叫做解方程组
代数部分
列方程(组)解应用题
知识点:
一、列方程(组)解应用题的一般步骤
1、审题:
2、设未知数;
3、找出相等关系,列方程(组);
4、解方程(组);
5、检验,作答;
代数部分
不等式及不等式组
知识点:
一、不等式与不等式的性质
1、不等式:表示不等关系的式子。(表示不等关系的常用符号:≠,<,>)。
2、不等式的性质:
(l)不等式的两边都加上(或减去)同一个数,不等号方向不改变,如a>b,c为实数a+c>b+c
(2)不等式两边都乘以(或除以)同一个正数,不等号方向不变,如a>b,c>0ac>bc。
(3)不等式两边都乘以(或除以)同一个负数,不等号方向改变,如a>b,c<0ac<bc.
注:在不等式的两边都乘以(或除以)一个实数时,一定要养成好的习惯、就是先确定该数的数性(正数,零,负数)再确定不等号方向是否改变,不能像应用等式的性质那样随便,以防出错。
代数部分
函数及其图像
知识点:
一、平面直角坐标系
1、平面内有公共原点且互相垂直的两条数轴,构成平面直角坐标系。在平面直角坐标系内的点和有序实数对之间建立了—一对应的关系。
2、不同位置点的坐标的特征:
(1)各象限内点的坐标有如下特征:
点P(x, y)在第一象限x >0,y>0;
点P(x, y)在第二象限x<0,y>0;
点P(x, y)在第三象限x<0,y<0;
点P(x, y)在第四象限x>0,y<0。
(2)坐标轴上的点有如下特征:
点P(x, y)在x轴上,y为0,x为任意实数。
点P(x,y)在y轴上,x为0,y为任意实数。
3.点P(x, y)坐标的几何意义:
(1)点P(x, y)到x轴的距离是| y |;
(2)点P(x, y)到y袖的距离是| x |;
(3)点P(x, y)到原点的距离是
4.关于坐标轴、原点对称的点的坐标的特征:
(1)点P(a, b)关于x轴的对称点是(a,-b);
(2)点P(a, b)关于y轴的对称点是(-a,b);
(3)点P(a, b)关于原点的对称点是(-a,-b);
二、函数的概念
1、常量和变量:在某一变化过程中可以取不同数值的量叫做变量;保持数值不变的量叫做常量。
2、函数:一般地,设在某一变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数。
(1)自变量取值范围的确是:

①解析式是只含有一个自变量的整式的函数,自变量取值范围是全体实数。
②解析式是只含有一个自变量的分式的函数,自变量取值范围是使分母不为0的实数。
③解析式是只含有一个自变量的偶次根式的函数,自变量取值范围是使被开方数非负的实数。
注意:在确定函数中自变量的取值范围时,如果遇到实际问题,还必须使实际问题有意义。
(2)函数值:给自变量在取值范围内的一个值所求得的函数的对应值。
(3)函数的表示方法:①解析法;②列表法;③图像法
(4)由函数的解析式作函数的图像,一般步骤是:①列表;②描点;③连线
代数部分
统计初步
知识点:
一、总体和样本:
在统计时,我们把所要考察的对象的全体叫做总体,其中每一考察对象叫做个体。从总体中抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本容量。
二、反映数据集中趋势的特征数
1、中位数:将一组数据接从小到大的顺序排列,处在最中间位置上的数据叫做这组数据的中位数,如果数据的个数为偶数中位数就是处在中间位置上两个数据的平均数。
2、众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。一组数据的众数可能不止一个。
几何部分
线段、角、相交线、平行线
知识点:
一、直线:直线是几何中不加定义的基本概念,直线的两大特征是“直”和“向两方无限延伸”。
二、直线的性质:经过两点有一条直线,并且只有一条直线,直线的这条性质是以公理的形式给出的,可简述为:过两点有且只有一条直线,两直线相交,只有一个交点。
三、射线:
1、射线的定义:直线上一点和它们的一旁的部分叫做射线。
2.射线的特征:“向一方无限延伸,它有一个端点。”
四、线段:
1、线段的定义:直线上两点和它之间的部分叫做线段,这两点叫做线段的端点。
2、线段的性质(公理):所有连接两点的线中,线段最短。
五、线段的中点:
1、定义如图1一1中,点B把线段AC分成两条相等的线段,点B叫做线段图1-1AC的中点。
2、表示法:
∵AB=BC
∴点B为AC的中点
六、角
1、角的两种定义:一种是有公共端点的两条射线所组成的图形叫做角。
要弄清定义中的两个重点
①角是由两条射线组成的图形;
②这两条射线必须有一个公共端点。另一种是一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。可以看出在起始位置的射线与终止位置的射线就形成了一个角。
2.角的平分线定义:一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。
七、角的度量:度量角的大小,可用“度”作为度量单位。把一个圆周分成360等份,每一份叫做一度的角。
八、角的分类:
(1)锐角:小于直角的角叫做锐角
(2)直角:平角的一半叫做直角
(3)钝角:大于直角而小于平角的角
(4)平角:把一条射线,绕着它的端点顺着一个方向旋转,当终止位置和起始位置成一直线时,所成的角叫做平角。
(5)周角:把一条射线,绕着它的端点顺着一个方向旋转,当终边和始边重合时,所成的角叫做周角。
(6)周角、平角、直角的关系是:l周角=2平角=4直角=360°
十、角的性质
1、对顶角相等。
2、同角或等角的余角相等。
3、同角或等角的补角相等。
十一、相交线
1、斜线:两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线。它们的交点叫做斜足。
2、两条直线互相垂直:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。
3、垂线:当两条直线互相垂直时,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
4、垂线的性质
(l)过一点有且只有一条直线与己知直线垂直。
(2)直线外一点与直线上各点连结的所有线段中,垂线段最短。简单说:垂线段最短。
十二、距离
1、两点的距离:连结两点的线段的长度叫做两点的距离。
2、从直线外一点到这条直线的垂线段的长度叫做点到直线的距离。
3、两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离。
说明:点到直线的距离和平行线的距离实际上是两个特殊点之间的距离,它们与点到直线的垂线段是分不开的。
十三、平行线
1、定义:在同一平面内,不相交的两条直线叫做平行线。
2、平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
3、平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
说明:也可以说两条射线或两条线段平行,这实际上是指它们所在的直线平行。
4、平行线的判定:
(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角互补,两直线平行。
5、平行线的性质
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
说明:要证明两条直线平行,用判定公理(或定理)在已知条件中有两条直线平行时,则应用性质定理。
6、如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
注意:当角的两边平行且方向相同(或相反)时,这两个角相等。当角的两边平行且一边方向相同另一方向相反时,这两个角互补。
几何部分
三角形
知识点:
一、关于三角形的一些概念
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
组成三角形的线段叫三角形的边;相邻两边的公共端点叫三角形的顶点;相邻两边所组成的角叫三角形的内角,简称三角形的角。
1、三角形的角平分线。
三角形的角平分线是一条线段(顶点与内角平分线和对边交线间的距离)
2、三角形的中线
三角形的中线也是一条线段(顶点到对边中点间的距离)
3.三角形的高
三角形的高线也是一条线段(顶点到对边的距离)
注意:三角形的中线和角平分线都在三角形内。
高线不一定在△内
4、三角形三条边的关系
三角形三边都不相等,叫不等边三角形;有两条边相等的叫等腰三角形;三边都相等的则叫等边三角形。
等腰三角形中,相等的两条边叫腰,另一边叫底边,腰和底边的夹角叫底角,两腰的夹角叫项角。
三角形中任意两边之和大于第三边,任意两边之差小于第三边。
推论三角形两边的差小于第三边。
不符合定理的三条线段,不能组成三角形的三边。
三、三角形的内角和
定理三角形三个内角的和等于180°
由定理可以知道,三角形的三个内角中,只可能有一个内角是直角或钝角。
推论1:直角三角形的两个锐角互余。
三角形一边与另一边的延长线组成的角,叫三角形的外角。
推论2:三角形的一个外角等于和它不相邻的两个内角的和。
推论3:三角形的一个外角大于任何一个和它不相邻的内角。
四、全等三角形
能够完全重合的两个图形叫全等形。
两个全等三角形重合时,互相重合的顶点叫对应顶点,互相重合的边叫对应边,互相重合的角叫对应角。
全等用符号“≌”表示
△ABC≌△A `B`C`表示A和A`,B和B`,C和C`是对应点。
全等三角形的对应边相等;全等三角形的对应角相等。
五、全等三角形的判定

1、边角边公理:有两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”)
注意:一定要是两边夹角,而不能是边边角。
2、角边角公理:有两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角“或“ASA”)
3、推论有两角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边’域“AAS”)
4、边边边公理有三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”)
由边边边公理可知,三角形的重要性质:三角形的稳定性。
除了上面的判定定理外,“边边角”或“角角角”都不能保证两个三角形全等。
5、直角三角形全等的判定:斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边,直角边”或“HL”)
六、角的平分线
定理1、在角的平分线上的点到这个角的两边的距离相等。
定理2、一个角的两边的距离相等的点,在这个角的平分线上。
由定理1、2可知:角的平分线是到角的两边距离相等的所有点的集合。
可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)
定理1:关于某条直线对称的两个图形是全等形。
定理2:如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线。
定理3:两个图形关于某条直线对称,如果它们的对应线段或延长相交。那么交点在对称轴上。
逆定理:如果两个图形的对应点连线被一条直线垂直平分,那么这两个图形关于这条直线对称。
十三、勾股定理
勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方
几何部分
圆
知识点:
一、圆
1、圆的有关性质
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆,固定的端点O叫圆心,线段OA叫半径。
由圆的意义可知:
圆上各点到定点(圆心O)的距离等于定长的点都在圆上。
二、直线和圆的位置关系
1、直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫圆的切线,唯一的公共点叫切点。
直线和圆没有公共点时,叫直线和圆相离。
2、若圆的半径为r,圆心到直线的距离为d,则:
直线和圆相交,d<r;直线和圆相切,d=r;直线和圆相离,d>r;
三、切线长定理
经过圆外一点可作圆的两条切线。在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫这点到圆的切线长。
切线长定理从圆外一点引圆的两条切线,它们的切线长相等。圆心和这一点的连线平分两条切线的夹角,
四、弦切角
顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角。
弦切角定:理弦切角等于它所央的弧对的圆周角。
推理如果两个弦切角所央的弧相等,那么这两个弦切角也相等。
五、和圆有关的比例线段
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
推理:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
六、两圆的公切线
和两个圆都相切的直线叫两圆的公切线,两圆在公切线同旁时,叫外公切线,在公切线两旁时,叫内公切线,公切线上两个切点的距离叫公切线的长。
相关文章
-
微商客户资源(微商货源网精准客源)详细阅读

微商找客源是对微商来说非常重要的一件事,很多做微商的就是苦苦支撑着因为没有客源,微商如何找客源一直是一个不衰的话题,下面我们就来讨论下这个话题。一:定...
2022-09-08 20986
-
什么是AR(什么是ar导航)详细阅读

增强现实的AR互动营销增强现实的AR互动营销一款叫做《口袋妖怪GO》的手游在欧美火了,在还未上线的中国,#PokemanGo#这一话题的微博阅读量已经...
2022-09-08 20054
-
弯弯的月亮像小船(弯弯的月亮像小船,小小的船儿两头尖)详细阅读

点击上方蓝字关注我们你拍一,我拍一,一个小孩坐飞机。你拍二,我拍二,两个小孩丢手绢。你拍三,我拍三,三个小孩来搬砖。你拍四,我拍四,四个小孩写大字。你...
2022-09-08 15098
-
流苏是什么(流苏是什么样子的图片)详细阅读

导语 听说流苏和秋天更配哦!流苏这个元素也不是今时今日才流行起来的,能经久不衰是因为它真的美呆了~踏进9月,秋高气爽,随风摇曳的流苏真心是风情万种!宝...
2022-09-08 744
-
淘口令是什么意思(什么叫做淘口令)详细阅读
现在开淘宝的越来越多了。但是做得好的好的始终还是那么多,好多人因为刚开始很迷茫,不知道怎么做,或者做到一半发现没有效果,无奈之下只好放弃了,我作为一个...
2022-09-08 791
-
发家致富网(发财致富网)详细阅读

前言:面相五行人格与性格职业密切相关,有什么用的性格就有什么样的命运,性格决定命运。有些人需要白手起家获得财富,有些人则有可能会发横财,你会通过什么方...
2022-09-08 771
-
兼职在家工作(在家工作的兼职)详细阅读

力哥说理财,简单又好玩。跟着力哥走,理财不用愁!本文3100字,阅读约6分钟我要介绍的赚钱工作就是兼职写稿赚稿费。主业靠写作发大财是件非常困难的事,只...
2022-09-08 793
-
系统流程图(系统流程图是描述)详细阅读
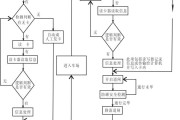
数据流程图(简称DFD)是一种能全面地描述信息系统逻辑模型的主要工具。简言之,就是以图形的方式来描述数据在系统流程中流动和处理的移动变换过程,反映数据...
2022-09-08 749

发表评论