黄金分割数(黄金分割数字是多少)

微博黄v号购买 2022年08月10日 04:51 96 admin

亲爱的A股训练营小伙伴们，晚上好。今日晚读我们将继续共读《艾略特波浪理论：市场行为的关键》，作者是小罗伯特 R.普莱切特&阿尔弗雷德 J.弗罗斯特。

黄金比率

黄金分割数(黄金分割数字是多少)

除数列中的头几个数字，任何一个数字与下一个数字的比大约是0.618比1,而与前一个数字的比值大约是1.618比1。随着数列的推移，比值就越接近于一个无理数即Phi.618034……数列中，两个间隔数字之间的比率是0.382,倒数是2.618。

Phi是唯一一个与1相加，可以得到其倒数的数字••〇.618+1=1-0.618。这种相加和相乘的结合，产生了以下等式序列：

0.6182=1-0.618,

0.6183=0.618-0.6182,

0.6184=0.6182-0.6183,

0.6185=0.6183-0.6184,等等或

=1+1.618,

=1.618+1.6182,

=1.6182+1.6183，

=1.6183+1.6184,

等等这四种比率的相关性质还可如下表示:1.618-0.618=1，

1.618x0.618=1,

1-0.618=0.382,

0.618xO.618=0.382,

2.618-1.618=1,

x0_382=1，

xO.618=1.618,

1.618xl.618=2.618

除了1和2,任何斐波那契数字乘以4,再有选择地加上一个斐波那契数字，就可以得到另一个斐波那契数字，如下：

3x4=12；+1=13,

展开全文

5x4=20;+1=21，

8x4=32;+2=34,

13x4=52；+3=55,

21x4=84;+5=89,

新数列展开过程中，第三个数列从它与4倍的乘积相加的数字开始。这种关系是存在的，因为隔两个数字的斐波那契数字间的比率是4.236,而0.236不仅是4.236的倒数，也是4.236与4的差。其他乘积产生了不同的数列，它们都基于斐波那契乘积。

黄金分割

任何长度都可以这样分割，即使较短部分与较长部分之间的比率，等于较长部分与整个长度之间的比率。这个比率永远是0.618。

黄金分割在自然界到处都是。事实上，从外形尺寸到面部排列，整个人体有着黄金分割。“在蒂迈欧篇中”，彼得•汤普金斯说,“柏拉图曾深人考虑过0>及其产生的所有数学关系中最紧密的黄金分割比例关系，并认为它是宇宙物理学的关键。”16世纪，约翰尼斯•开普勒在谈到黄金分割或称“神赐分割”时，说它实质上描绘了万物，尤其象征着“特征传递”的上帝造化。人体可以在肚脐处形成黄金分割。统计上的平均值大约是0.618。这个比率对男女都一样，是一种“特征传递”的完美标志。人类的进步是不是也是一种“特征传递”的创造呢？

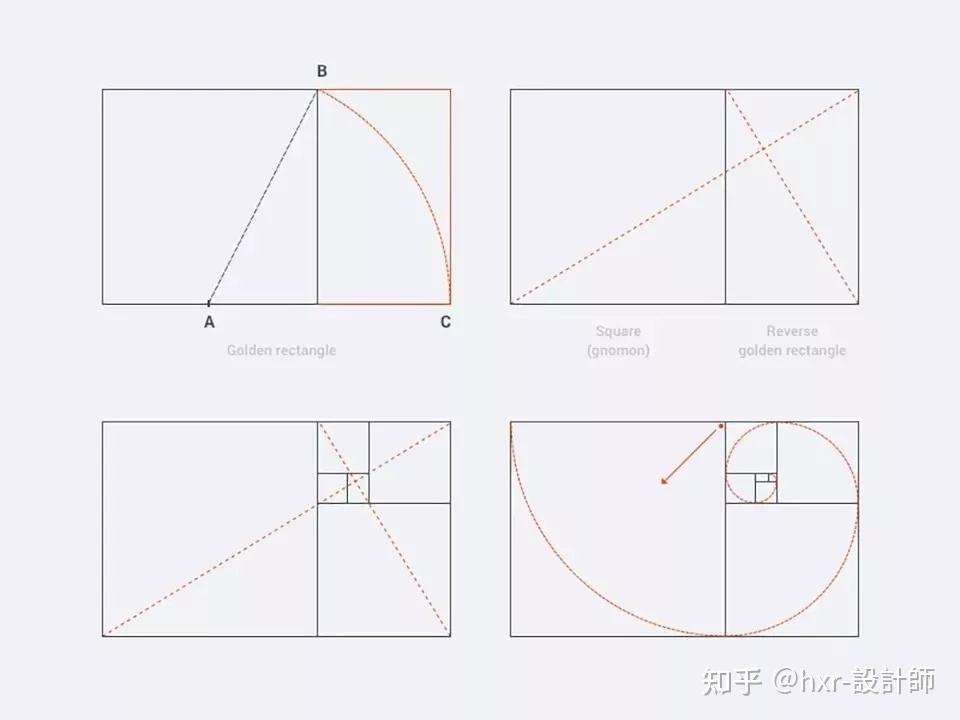
黄金矩形

黄金矩形相邻两边之比是1.618:1。要构建一个黄金矩形，首先得画一个两个单位长度乘两个单位长度的正方形，然后从正方形一边的中点至对边直角的顶点作一条连线。

三角形EDB是一个直角三角形。大约在公元前550年，毕达哥拉斯曾证明，直角三角形的斜边（X)的平方等于另外两边的平方和。因此，在本例中,X2二22+I2,或X2二5。所以，线段EB的长度一定是5的平方根。构建黄金矩形的下一步是延长线段CD，使EG的长度等于5的平方根或2.236个单位长度，如图3-5所示。此时，矩形的边呈黄金比率，矩形AFGC和矩形BFGD也都是黄金矩形。

矩形的边呈黄金比率，所以这个矩形被定义为黄金矩形。

黄金矩形大大丰富了艺术领域。在古埃及、古希腊和文艺复兴这些文化顶峰时期，黄金比的价值与应用非常广泛。莱昂纳多•达•芬奇对黄金比率做出了重要贡献。他也发现这种比率会令人愉快,并说道，“如果一件东西外形不协调，它就不可能完美”。达•芬奇的许多绘画作品外形协调，因为他有意识地用黄金比例来增强作品的表现力。古代和现代的建筑师，尤其是那些设计雅典巴台农神庙的著名建筑师，都成功地把黄金矩形运用到他们的设计之中。

显然，比率确实对形态的观察者产生影响。试验已证实，这个比例在美学上有舒适感。例如，让实验人员从一组不同类型的矩形中挑选出一个，平均来说，都会选择接近黄金矩形的形状。如果要求实验人员用他们最喜欢的方式，将一根杆子与另一根杆子交叉，通常划分比例为。窗户、画框、建筑、书籍以及墓地的十字架的比例都近似于黄金矩形。

如同黄金分割一样，黄金矩形的价值不仅仅只限于美学，显然还有其他作用。所有的例子中最有说服力的就是，DNA的双螺旋结构在旋转的间隔处呈精确的黄金矩形状。

黄金分割与黄金矩形代表了自然界和人造的美学及工用的静态形态，而要体现舒适的美学活力，一种生长或发展的有序过程，则莫属黄金螺线一一宇宙中最独特的形态之一,最为合适了。

黄金螺线

黄金矩形可以用来构造黄金螺线。任何一个黄金矩形，如图3-5中所示,都可被划分成一个正方形和一个较小的黄金矩形，如图3-6所示。理论上这个细分过程可以无限延伸。

图3-6

本身互为黄金比例的两条虚线，对角平分了矩形，它们的交点正是正方形旋转的理论中心。在靠近中心点处，可以绘制一条如图3-7所示的螺线，即按正方形增大的方向，连接每个旋转正方形的交叉点形成一条曲线。当正方形向内或向外旋转时，它们的连接点就描绘出了一条黄金螺线。在黄金螺线形成中的每一点,弧长与直径的比都是1.618。

共读作者：陆海，是我们A股训练营2营的群友。在国内一家上市金融公司从事经营分析工作。入市20余年，力求尽可能接近缠论，无欲无求、心如明镜，完美折射市场行为的境地。

他的学习建议：“志不强者智不达，学习讲究“穷源”，探索其根源，找到该理论有效性的保证。前言一开始引用圣经中的话，就是该理论的“源”。艾略特波浪属形态学，其预测准确性由永恒的人性，导致事物发展的重复，所保证。所有章节均同等重要。如果，初学者可以先把握第１、２章，然后花上半年左右的光阴，手工绘制几百张，不同指数与商品的60分钟波浪图，经过深度思考后，再接着学习后续章节，效果更佳。”

黄金分割数(黄金分割数字是多少)